Let's make the following definition:
If T is a binary tree with root r, then its rank is
- 0 if r has no children
- 1+q if r has two children, both with rank q
- otherwise, the maximum rank of any of the children
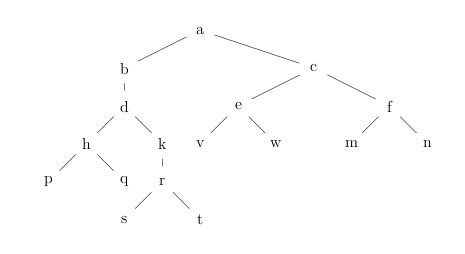
(a) Compute the rank of each subtree in the following tree:

Hint: for each subtree, write the rank on its root. Start with the leaf nodes and work upwards in the tree.
Check your solution before you do parts (b) and (c), to make sure you correctly understand the definition of rank.
(b) For a given height h, what shape of tree has the largest rank? smallest rank?
Check your solution before you do part (c).
(c) Use induction to prove the following claim:
Claim: a tree with rank q has at least \(2^q\) leaves
Check the outline of your solution.
Check your full solution.
Let's define the grammar G as follows:
\(S \ \rightarrow \ a \ \mid\ aB \)
\(B \ \rightarrow \ aaS \ \mid\ BB \)
Notice a tree generated by G has a terminal string of the form \(a^n\) i.e. n copies of the terminal value a. Prove that n is congruent to 1 (mod 3).
Hint 1: you can handle the modular arithmetic informally. Concentrate on building a good outline for the tree induction.
Hint 2: let's define the notation L(T) to be the length of the terminal string of tree T.
Hint 3: you may wish to strengthen the claim, i.e. modify your grammar and claim to cover a wider range of trees. (WTF? Here are some hints.)
Check against the solution.
A free tree is a connected (undirected) graph that contains no cycles. So it has a tree-like structure, but no root and no left-to-right ordering on its nodes. A free tree spans a graph G if it is a subgraph of G and contains all of G's nodes. It is also called a spanning tree of G,
Let us define a function f as follows: $$ \begin{equation} f(n) = \begin{cases} 1 \quad when \quad n = 0 \\ \\ 2^{n-1} (f(n-1))^2 \quad when \quad n \geq 1 \\ \end{cases} \end{equation} $$
Prove that for any hypercube \(Q_{n}\) (\(n \geq 0\)) there are at least f(n) distinct free trees that span \(Q_{n}\).
Stuck? Here are some hints.
Check against the solution.
Flatlander Chocolates makes rectangular chocolate bars, each divided into a p by q grid of squares. We can break a chocolate bar in two along one of the grid lines. Prove that it takes pq-1 breaks to divide a chocolate bar into individual squares.
Stuck? Here are some hints.
Check against the solution.