Discrete Structures (CS 173)
Margaret Fleck, University of Illinois

|
Discrete Structures (CS 173)
|
I have been developing Discrete Structures course materials since Fall 1991 and have taught this course 29 times, ranging from 60-person classes in the 1990's to an 800-person offering in Spring 2021. At the University of Illinois, this course is taught right after one term of programming and one term of calculus, so it's critical that the course be accessible to students with limited background but prepare them for subsequent theoretical CS courses. We make extensive use of canned online materials and automated grading due to our size and recent pandemic restrictions. But key activities (notably tutorials) are run live for the benefit of students and we provide strong support for manual grading of proofs and problems requiring justification.
My textbook Building Blocks for Theoretical Computer Science was written for this course and is available online. Since its introduction in 2012, it has been picked up by major repositories of online books, is recommended by course syllabi at academic institutions ranging from Harvard to Hacettepe University, and even has a review (4.5/5 stars!) on goodreads.com. It is more concise than the commonly used text by Rosen and it spreads the difficult topic of proof construction across the term rather than hoping students can quickly absorb it in the first couple weeks. Early in the term, we use only variants of direct proof, to teach basic skills such as logical order and substitution of definitions. Other major outlines (induction, two-way bounding, contradiction) are introduced much later. This allows applications (e.g. graphs) to be introduced early and used to help motivate the proof construction techniques.
This course expects students to attempt the assigned readings before lecture. So we have a relatively short amount of lecture (75min per week) which concentrates on concepts that are harder to understand. The lecture page for a recent offering shows the sequence of topics, along with our covid-lockdown lecture videos and written-up lecture notes. I recommend looking at
For those who have heard about the course, the Recursion Fairy appears late in the second induction lecture. (Mediaspace audio sometimes echoes. If so, try switching browser.)
Specific issues involved in teaching this material well include
An innovative feature of the course (since 2014) is the use of weekly small assessments ("examlets"). Frequent assessment evens out the workload and provides an incentive for students to do self-graded practice problems. The final exam is short, the equivalent of two weekly examlets. For each examlet, students are given an explicit skills list and TAs are given a pre-built rubric for grading open-answer questions.
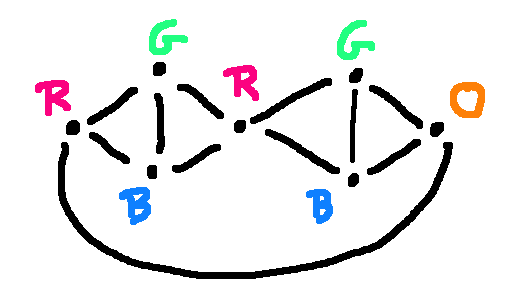
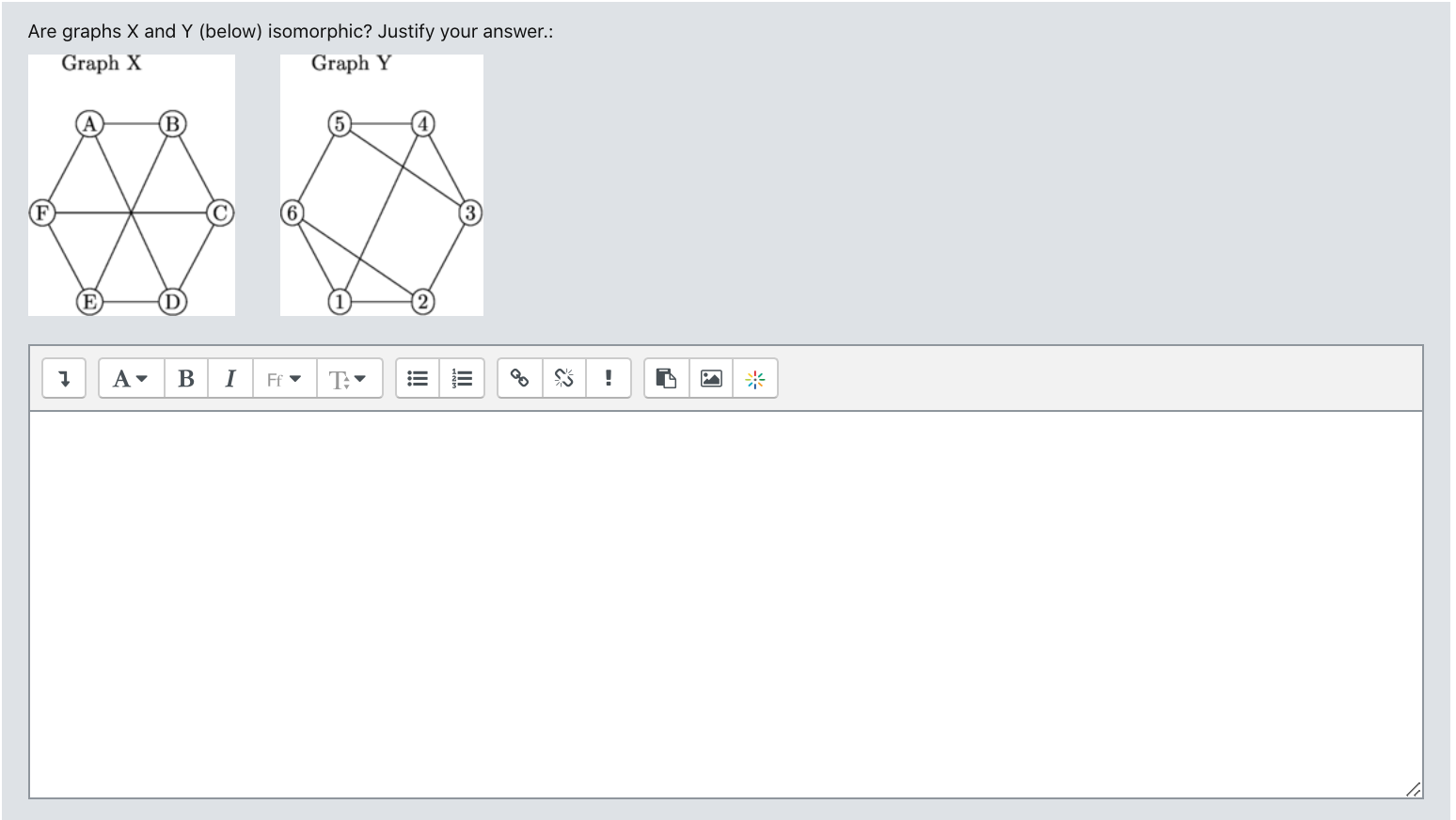
The examlets contain a mixture of multiple choice, drag and drop, short answer questions, shown below. For long proof questions (not shown), the interface allows students to include typeset equations in their answers. Open-answer questions include model solutions, vital for course staff grading questions that may have many variants.
|
|
|
Examlets are heavily randomized to discourage both cheating and blind memorization. I have built a bank of about 2000 questions, with hooks for cosmetic variation (e.g. changing the type of object to be counted in a word problem). These are stored offline in a human-friendly YAML format, from which we can generate latex macros for making randomized hardcopy exams and also convert the questions into the upload formats for two LMS systems (Moodle and PrairieLearn). (See here for more details.)
Each random question is drawn from a set of variants large enough (typically over 20) that there will be variation in difficulty. Similarly, even good rubrics do not entirely eliminate variation in grading between TAs. However, the exam sequence involves enough independent random choices over the course of the term (25 for hardcopy offerings, 85 for online) to reliably average out these types of variation.
Writing proofs fluently requires practice. We provide three types of practice explicitly, and students quickly discover a fourth.
This page from a recent offering shows a typical sequence of tutorials and study problems.
The weekly examlets provide a strong incentive to use these practice materials. Therefore much of this practice is offered on the honor system, contributing relatively little (in some cases nothing) to a student's course average. This allows us to offer a static, carefully curated set of problems that draws on many years of staff creativity. Before the examlet system, homework construction had become an arms race where course staff burnt a lot of manpower trying to create novel problems so students could not copy solutions.
These materials would not exist without my wonderful course staff and co-instructors. In the sections I've taught or worked closely with, I've collaborated with 12 instructors, 3 acting instructors, over 100 TAs (four of whom won departmental teaching awards for the course), and over 70 undergraduate course assistants. In particular, Eric Shaffer co-taught the first two offerings of the course with the new topic order. Most of the study problems started life as homework problems, written by a wide range of TAs and co-instructors. The first set of online homework problems were created jointly by Lenny Pitt and myself. Lance Pittman did considerable work improving that collection and co-authored the booklet of tutorial/discussion problems.
Here are the web sites for several previous offerings:
University courses recommending the textbook:
Other recommendations
My favorite review was by a student at Florida Atlantic University in 2012:
I'm a Sophomore Computer Science student at Florida Atlantic University and currently taking Discrete Math.
Unfortunately for me, my Discrete Math teacher is a visiting instructor from Japan whom I have a lot of trouble understanding and ironically (or not?), she doesn't understand most of what I ask either.
To further complicate matters, our assigned textbook is unusually vague and teaches from a higher level of understanding than anyone would expect from a Discrete Math class with no pre-requisites (FAU doesn't require any at all for Discrete Math).
To make a long story short: after just about failing my first Exam and continuing to struggle to understand between the text and my instructor I was in peril, ready to drop the class (and honestly even re-evaluating my path in Computer Science). I took to the internet, specifically reddit.
Within 20 minutes I stumbled across the link to your class, http://courses.engr.illinois.edu/cs173/fa2011/ .
I would like to take this opportunity to give you an immense THANK YOU! If not for your lecture notes (as they go in the exact order as our class, but with much more detail and better explanation). I would likely be dropping this class and still be feeling as if Discrete Math is some horribly abstract subject that I will never be able to understand. All of a sudden, it all sounds a lot less like gibberish.
So, again, as I can not say it enough: THANK YOU! You have quite conceivably just saved my career in Computer Science.