Two-way-bounding study problems

Problem 1

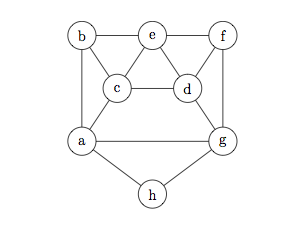
What is the chromatic number of the following graph? Justify your answer.

solution

Problem 2

(Do problem 1 and check your solution before attempting this problem.)

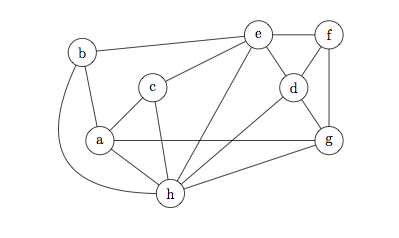
What is the chromatic number of the following graph? Justify your answer.

solution

Problem 3

Let's define sets A and B as follows:

• \(A = \{(x,y) \in \mathbb{R}^2 : y = 3x + 7\} \)
• \( B = \{\lambda(-2,1) + (1-\lambda)(1,10) : \lambda \in \mathbb{R}\}\)

Prove that A=B.

Hint: this is in the two-way bounding section. What technique do you think we want you to use?

solution

Problem 4

Recall that if G is a graph, then \(\chi(G)\) is its chromatic number. Suppose that P is a connected graph and G is another connected graph, not connected to P. Now, create a new graph M which consists of a copy of P, a copy of G, and a new edge that connects some vertex of P to some vertex of G. For example, suppose that P is \(C_5\) and G is \(K_4\). Then M might look as follows, where g marks vertices of G and p marks vertices of P, and the new edge is the dashed line.

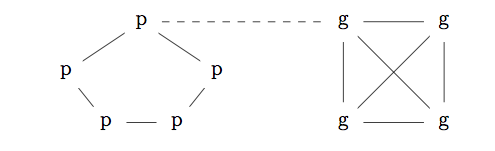
Give a formula expressing \(\chi(M)\) in terms of \(\chi(P)\) and \(\chi(G)\)? Be as precise as possible and justify your answer.

hints

solution