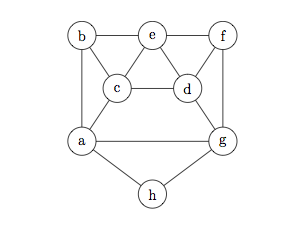
Here's the graph again for reference:

The chromatic number of this graph is 4.
Upper bound: from the following picture, you can see that four colors is sufficient.
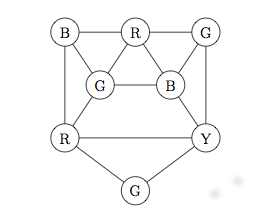
Lower bound: we'll try to color this graph with only three colors and show that this cannot work. Since the nodes a, b, and c are all connected to one another, they must have three different colors. Since it doesn't matter which color is which, let's fix these as
Since node e is adjacent to blue and green nodes, it must be colored red. Since node d is adjacent to green and red nodes, it must be colored blue. Since node f is adjacent to red and blue nodes, it must be colored green.
But now we are stuck: node g is adjacent to a red node, a blue node, and a green node. Since all of our coloring decisions were forced by the structure of the graph, it's not possible to color the whole graph with only three colors.
Another way to argue the lower bound is to note that this graph contains the special graph at the end of section 10.3 in the textbook, which was shown to have chromatic number 4. To find this subgraph, delete node h, as well as the edges ah, gh, and cd. Notice, however, that this argument will only work if you know that the reader is familiar with this particular special graph (e.g. has read this particular textbook).